P=NP, le problème qui peut vous rendre riche

Quel geek n’a jamais entendu parler du célèbre problème P=NP ? Cette question, qui mêle informatique et mathématique et fait partie des 7 problèmes du millénaire, n’a à ce jour pas été résolue, malgré qu’elle soit connue depuis pas loin d’un demi-siècle par les chercheurs. P=NP constitue une exception dans la liste des problèmes les plus difficiles, car il est relativement simple à comprendre pour un amateur, malgré qu’il cache des rouages puissants et complexes. Celui ou celle qui le résoudra se verra attribuer un prix de 1 million de dollars et pourra utiliser ce savoir dans son propre intérêt, par exemple pour miner une énorme quantité de Bitcoins à vitesse grand V. Cela permettra plus généralement d’accélérer les méthodes de calculs des ordinateurs actuels. Découvrez donc ce qui fait la force de ce problème, et les conséquences qu’impliquerait sa résolution.

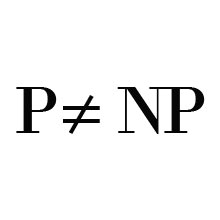
P=NP ou P\=NP ? Telle est la question. Mais avant de tenter de résoudre l’une des conjectures les plus importantes des mathématiques, attachons-nous à en comprendre le sens.

Que signifie P ? Et NP ? (Partie 1)

Regardons tout d’abord ce que nous dit Wikipédia : « il s’agit de savoir si la classe de complexité P des problèmes de décision admettant un algorithme de résolution s’exécutant en temps polynomial sur une machine de Turing est équivalente à la classe de complexité NP des problèmes de décision dont la vérification du résultat, une fois celui-ci connu, demande un temps polynomial. ». Incompréhensible pour la plupart d’entre nous. Mais comme je vous ai indiqué que le problème était compréhensible pour un débutant, je vais tâcher de vous l’expliquer avec des mots simples.

La théorie de la complexité comme arme de mesure

Pour comprendre ce que signifient P et NP, vous devez comprendre quelques concepts de base de l’informatique théorique, plus précisément de la théorie de la complexité. En informatique théorique, on étudie la complexité des algorithmes : elle se mesure sur le temps et la mémoire que prend un algorithme pour s’exécuter. Pour la calculer, on compte le nombre d’opérations élémentaires (additions, multiplications, lecture d’entrée, test de condition, etc.) que l’algorithme effectue. On note cette complexité O(n), n étant la quantité de données d’entrées. La plupart du temps, ce n’est pas simplement « n » entre parenthèses mais souvent n avec d’autres termes, comme 2n ou n³. Par exemple, un algorithme qui prend en entrée une liste d’entiers (comme 3, 9, 4, 94, 7) et qui parcourt cette liste un nombre de fois équivalent à la taille (taille : nombre d’éléments contenus dans la liste) de la liste, aura une complexité en O(n²) : quand il parcourt la liste de taille n une fois, il fait n opérations. Et comme il effectue ce parcours n fois, cela fait n * n opérations, soit n² ! Ainsi, on peut évaluer la rapidité et l’efficacité d’un algorithme via sa complexité, ce qui est très utile dans la résolution de problèmes avec beaucoup de données.

Ensuite, une fois les complexités calculées, on peut déterminer quel problème algorithmique nécessite quelle complexité, c’est-à-dire quel problème nécessite quelle quantité de ressources pour qu’un calcul efficace apporte une réponse. Car certains problèmes ont énormément de données, comme des liste d’entiers de taille 1 milliard, ce qui ferait 1 milliard * 1 milliard d’opérations avec notre algorithme précédent, ce qui ferait un temps d’exécution de 541 ans avec un ordinateur moderne… C’est là qu’interviennent les classes de complexité : on classe ces problèmes par la quantité de ressources qu’ils nécessitent, et ceux qui nécessitent la même quantité sont disposés dans la même classe de complexité. Cependant, détailler toutes les classes de complexité qui existent me prendrait trop de temps, et ce n’est pas le but de cet article. En effet, les seules classes qui nous intéressent ici sont la classe P et la classe NP.

Que signifie P ? Et NP ? (Partie 2)

Maintenant que vous avez (à peu près) compris les bases de l’informatique théorique, je peux vous donner la signification de ces 2 mots. Car oui, P signifie polynomial, ce qui signifie que l’on peut rapidement trouver une solution (grâce à un algorithme qui s’exécute en temps polynomial, donc rapidement) aux problèmes appartenant à cette classe. Les problèmes de la classe NP (pour non déterministe polynomial), quant à eux, sont classés ainsi car on peut rapidement prouver qu’une solution proposée pour l’un d’eux est valide. Le fait de poser P=NP revient donc à demander si pour tous les problèmes dont une solution peut être vérifiée rapidement, cette même solution peut être trouvée rapidement. Si vous avez compris cela, vous avez compris l’un des problèmes les plus durs des mathématiques actuelles, que de nombreux chercheurs ont tenté de résoudre sur plusieurs générations, en vain (pour l’instant). Voyons maintenant pourquoi la résolution de ce problème est si importante, et les avancées scientifiques qu’elle permettrait.

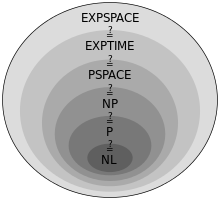
Pourquoi résoudre P=NP ?

Il y a trois manières de résoudre ce problème : prouver P=NP, P\=NP, ou démontrer que ce n’est pas démontrable. Le plus intéressant ici serait évidemment de prouver P=NP. Mais regardons d’abord ce qu’impliquerait P\=NP. Cela signifierait que certains des problèmes les plus durs de l’informatique n’ont pas de solution rapide (en temps polynomial). Et, de manière plus concrète, cela montrerait qu’il est impossible que faire mieux que de la « force brute » pour certains problèmes, et de plus, certains domaines, comme la sécurité bancaire, seraient assurés (car elle se base sur le fait qu’il n’existe pas d’algorithme en temps polynomial, qui puisse donc casser ses clés). Plus généralement, une preuve de P\=NP, signifierait qu’il est plus difficile de chercher une solution à un problème que vérifier qu’une réponse donnée à ce problème est correcte. Mais là où les choses deviennent intéressantes, c’est dans le cas où quelqu’un parvenait à prouver P=NP.

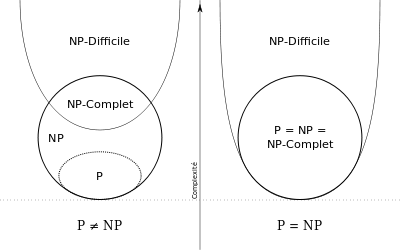
Car oui, la preuve de P=NP permettrait des progrès exceptionnels et insoupçonnés dans l’informatique moderne. Elle permettrait la résolution de problèmes réputés comme étant très durs, qui n’ont pour l’instant pas de solution efficace. Et ce ne serait pas un phénomène isolé, car ces problèmes concernent notre vie de tous les jours : ils sont impliqués dans des domaines publics comme la biologie ou l’économie. Cela entraînerait donc des prouesses majeures dans de nombreuses sphères autres que l’informatique. À l’inverse de P\=NP, cela provoquerait la chute de secteurs comme la sécurité bancaire ou la cryptographie. Plus généralement, les ordinateurs verraient leur capacité de calcul se décupler et devenir bien plus rapides. La résolution d’un sudoku par une machine serait par exemple quasi instantanée, comparé au temps qu’elle prend aujourd’hui. Mais outre que des progrès énormes, la résolution de P=NP pourrait vous rendre très riche.

P=NP=beaucoup d’argent

Premièrement, comme il fait partie des 7 problèmes du millénaire, vous vous verriez attribuer la modique somme d’1 million de dollars. Ce qui est peu, me direz vous, comparé aux avancées technologiques provoquées. Scott Aaronson, qui travaille dans le domaine de l’informatique théorique, a déclaré lors d’une conférence : « Si quelqu’un prouve que P=NP, la première chose qu’il devrait faire c’est de voler 200 milliards de dollars en Bitcoin. La seconde chose qu’il devrait faire c’est de résoudre les autres problèmes du prix du millénaire. ». Car le fait de prouver cette conjecture vous permettrait d’utiliser sa solution dans un but très lucratif : vous pourriez miner du Bitcoin très rapidement, et donc vous enrichir très rapidement. Ce qui entraînerait un effondrement du cours de celui-ci, si vous publiez sa solution. Vous deviendrez donc la personne la plus riche du monde, et seriez doté d’un pouvoir économique, technologique et politique incroyable. Mais ce scénario est évidemment utopique, et pour parvenir à la résolution d’un tel problème, vous devrez faire preuve de plus d’intelligence que tous les brillants scientifiques qui se sont essayés à cette preuve.

Conclusion

Prouver P=NP, c’est apporter des réponses à de nombreuses problématiques actuelles, que ce soit dans des domaines appliqués comme l’industrie ou plus théorique comme les mathématiques. C’est offrir une meilleure compréhension du monde contemporain et faire un pas de géant dans la recherche en informatique théorique. C’est répondre de manière correcte à un des 7 problèmes du millénaire et à une des questions ouvertes les plus célèbres de l’histoire. Et plus personnellement, c’est recevoir la reconnaissance de millions de gens et de s’enrichir de manière drastique. Mais pour y parvenir, il faudra sûrement encore de nombreuses années de recherche et d’études, et qui sait, peut-être êtes-vous le/la futur(e) personne qui parviendra à cet exploit ? Car comme l’a dit Albert Einstein, un problème sans solution est un problème mal posé, donc ne désespérez pas.

J’espère avoir éveillé votre curiosité vis-à-vis de ce passionnant et gigantesque domaine qu’est l’informatique théorique ainsi que les mathématiques, et vous avoir donné l’envie de trouver une solution à cette difficile mais magnifique question. Si c’est le cas, je vous met plusieurs liens sur le sujet :

Un site qui recense toutes les solutions proposées (et invalides)  au problème : https://www.win.tue.nl/~gwoegi/P-versus-NP.htm

La page Wikipédia sur P=NP : https://fr.wikipedia.org/wiki/Probl%C3%A8me_P_%3D_NP

La page Wikipédia sur la théorie de la complexité : https://fr.wikipedia.org/wiki/Th%C3%A9orie_de_la_complexit%C3%A9_%28informatique_th%C3%A9orique%29

Attention : toutes les solutions que vous pourrez trouver sur Internet sont a priori fausses. Chaque mois, plusieurs amateurs proposent des solutions à P=NP, ce qui provoque en général l’hilarité des chercheurs. Attention donc à ne pas prendre au sérieux ces « preuves ». Il peut cependant être intéressant des les lire si vous êtes intéressé par les mathématiques et l’informatique.